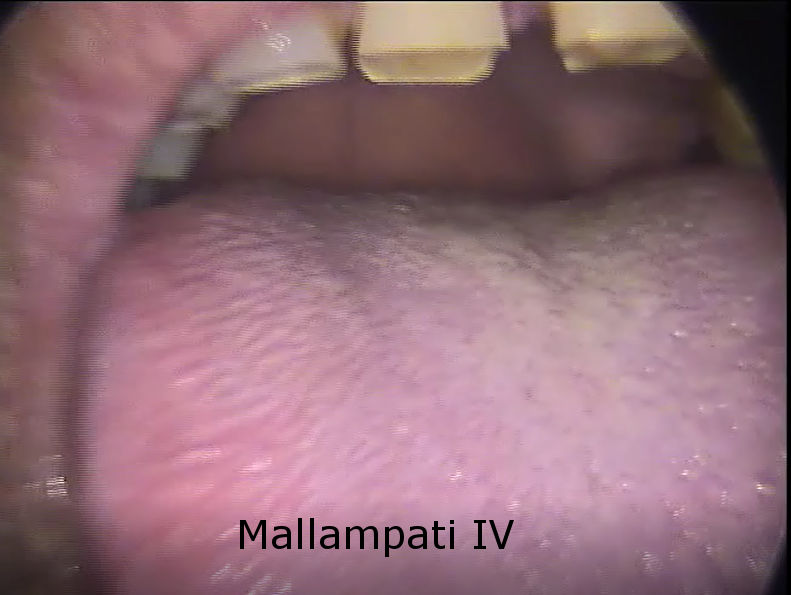
 PREDICCIÓN DE LA DIFICULTAD DE INTUBACIÓN APLICABLE A CUALQUIER PACIENTE EN COMPARACIÓN CON UN ESTUDIO SIMILAR QUE NO INCLUYE VARIABLES NUMERICAS.
PREDICCIÓN DE LA DIFICULTAD DE INTUBACIÓN APLICABLE A CUALQUIER PACIENTE EN COMPARACIÓN CON UN ESTUDIO SIMILAR QUE NO INCLUYE VARIABLES NUMERICAS.
Predicción de la dificultad de intubación mediante un análisis de regresión logística.
Resumen
Introducción y objetivos: El objetivo de este trabajo es predecir la dificultad de intubación mediante un análisis de regresión logística, que incluye variables numéricas y contrastarlo con un ensayo previo que no las incluye y comprobar si al añadir éstas a las variables categóricas ya estudiadas, sigue siendo válido para su objetivo y se puede aplicar a cualquier paciente de fuera del estudio.
Material y Métodos: En 300 pacientes, además de las variables categóricas investigadas en un estudio anterior para encontrar un método de predicción de dificultad de intubación en cualquier paciente, se añadieron las siguientes variables cuantitativas: índice de masa corporal, distancia tiromentoniana, apertura de la boca y tamaño del cuello en cm, además de la edad en años. Se realizó con ellas y las anteriores categóricas, incluida el resultado de una Laringoscopia Indirecta, un análisis de regresión logística. Se aplica el modelo a cualquier paciente mediante la inserción en la barra de fórmulas en Excel de una función dada.
Resultados: El modelo encontrado y sus coeficientes para confeccionarlo fueron: f(x) = 1,371 + 2,481 Laringoscopia Indirecta (3-4) + 2,181 Distancia Tiromentoniana <6,5cm + (-1,484* cm Apertura Boca). En relación con el estudio anterior además de presentar distintos coeficientes en las variables categóricas, el modelo sustituye la variable categórica apertura de la boca < 3,5 cm por su correspondiente variable cuantitativa. La probabilidad teórica (y) asociada a un paciente de encontrarnos con una dificultad de intubación es y = e f(x)/(1+e f(x)) y aplicándolo a Excel =EXPf(x)/(1+EXPf(x)). La ecuación aquí también se puede utilizar para cualquier paciente.
Conclusiones: Como en el ensayo anterior la Laringoscopia Indirecta fue la variable independiente con más poder predictivo, la inclusión de las variables cuantitativas no varía lo anterior pero amplía los resultados.
Palabras clave: Predictor; Laringoscopia Indirecta; Laringoscopio Rígido; Laringoscopia Directa; Vía Aérea Difícil.
Prediction of difficult intubation (3).
Prediction of difficulty intubation applicable to any patient compared to a similar study that does not include numeric variables.
Prediction of difficult intubation using a logistic regression analysis.
Summary
Introduction and Objectives: The aim of this study is to predict difficult intubation using a logistic regression analysis that includes numeric variables and contrast with a previous trial that does not include them and check whether adding them to categorical variables and studied, follows still valid for its purpose and can be applied to any patient outside the studio.
Material and Methods: 300 patients, and categorical variables investigated in an earlier study to find a method of predicting difficult intubation in any patient, the following quantitative variables added: BMI, thyromental distance, opening mouth and neck size in cm, besides age in years. It was performed with them and the above categorical, including the result of indirect laryngoscopy, logistic regression analysis. the model is applied to any patient by inserting into the formula bar in Excel of a given function.
Results: The model coefficients and found to tailor it were: f (x) = 1.371 + 2.481 indirect laryngoscopy (03/04) + 2.181 thyromental distance <6,5cm + (-1.484 * cm opening mouth). In the previous study besides presenting different coefficients categorical variables, the model replaces the categorical variable mouth opening <3.5 cm for the variable corresponding quantitative. Theoretical probability (y) associated with a patient to meet with difficult intubation is y = f (x) / (1 + e f (x) ) and applying it to Excel = EXPf (x) / (1 + EXPf ( x)). The equation here also can be used for any patient.
Conclusions: As in the above test the indirect laryngoscopy was the independent variable with more predictive power, including quantitative variables varies above but extends the results.
Keywords: Predictor; Indirect laryngoscopy; rigid laryngoscope; Direct laryngoscopy; difficult airway.
Introducción.
El análisis de regresión logística se utiliza para predecir el resultado de una variable categórica en función de otras variables independientes categóricas o cuantitativas1. En un estudio anterior2, lo aplicamos en 300 pacientes sometidos a anestesia general, para predecir cuáles de ellos iban a presentar una dificultad de intubación practicada mediante Laringoscopia Directa (LD), en función de otras variables: parámetros antropométricos (IMC, DTM, tamaño del cuello y Apertura de la Boca) y pruebas predictoras de vía aérea difícil, a las que se añadió el resultado de la exploración mediante Laringoscopia Indirecta (LI), todas ellas transformadas en variables categóricas. La función resultante verificamos que se podía adaptar a cualquier paciente de fuera del ensayo y que la LI fue la variable con más potencia (mayor coeficiente).
En el ensayo anterior2, para intentar minimizar los factores de confusión, en vez de introducir las variables manualmente se optó por dejar que el programa SPSS hiciera automáticamente la regresión por el procedimiento Adelante RV, en este utilizamos el mismo método. No obstante, para ampliar el estudio y comprobar sus limitaciones sería conveniente investigar que ocurre si se añaden como variables independientes en el análisis de regresión logística, las variables cuantitativas que en el anterior se habían transformado en categóricas.
Así pues el objetivo de este estudio es contrastar con otro expuesto anteriormente, si añadiendo las variables cuantitativas como tales, además de todas las categóricas ya investigadas, la función obtenida como resultado es válida para para predecir la dificultad de intubación en cualquier paciente de fuera del estudio y si la LI sigue siendo la variable con más potencia.
Material y métodos.
Se utilizaron los mismos parámetros del ensayo anterior y las mismas pruebas de evaluación de la vía aérea. Sólo hay que añadir que en el análisis de regresión logística se introdujeron las siguientes variables cuantitativas: Edad en años, Indice de Masa Corporal, Distancia Tiromentoniana, Apertura de la Boca y tamaño del cuello en cm y se añadieron a las categóricas ya estudiadas (Tabla 1).
También en primer lugar, se exploró la asociación y se estimó la significación estadística que existe entre los predictores clínicos, demográficos y la LI, con la dificultad de intubación observada mediante LD.
De la misma manera para valorar la potencia de la LI como predictor de la dificultad de intubación e investigar qué variables explicativas o independientes (predictores antropométricos, demográficos, clínicos y la LI) se relacionan con la variable respuesta o dependiente , se realizó un análisis de regresión logística.
Con los coeficientes encontrados, se realizó un modelo f(x) en cada caso, para determinar la probabilidad teórica (y) asociada a un paciente de encontrarnos con una dificultad de intubación, y = e f(x)/(1 + e f(x)) e igualmente que en el estudio previo extrapolándolo a Excel la función a aplicar sería==EXPf(x)/(1+(EXPf(x)).
Para determinar si el modelo propuesto puede considerarse aceptable y puede explicar lo que se observa, se evalúa la distancia entre lo observado en los datos que tenemos en la realidad y lo esperado bajo el modelo, para ello se aplica tanto en este estudio como en el anterior el test de Hosmer-Lemeshow. Si hay una elevada coincidencia entre observados y esperados, el test de Chi-cuadrado no mostrará significación estadística y el modelo presenta un buen ajuste.
Con la probabilidad teórica o pronosticada en cada paciente de encontrarnos ante una dificultad de intubación se confeccionó la curva COR (característica operativa del receptor), para compararla con la curva obtenida en el anterior ensayo.
También se realizó un gráfico de cajas para observar las diferencias entre las cifras de probabilidad pronosticada entre los pacientes con dificultad de intubación y sin ella y así mismo observar las diferencias con el gráfico de cajas obtenido anteriormente.
Los datos se analizaron con el programa SPSS 15® para Microsoft Windows®. Los resultados se expresan como media, mediana (rango) y frecuencia. El valor de significación estadística se asumió cuando p<0,05.
Resultados.
En la Tabla 1 se contemplan todas las variables cuantitativas y categóricas que hemos introducido en el análisis de regresión logística para obtener la ecuación, se observa entre las cuantitativas que la DTM y la Apertura de la Boca son las únicas con significación estadística (<0,005). En cuanto a las categóricas son las mismas que en el artículo anterior.
En la Tabla 2 se pueden observar los resultados del análisis de regresión logística, la relación y la potencia de las variables independientes con la variable dependiente dificultad de intubación. Proporciona un resultado correcto en el 96 % de los casos.
En la Tabla 3 se contemplan las cifras de probabilidad pronosticada obtenidas de los diferentes pacientes y su par asociado de sensibilidad y 1-especificidad. Con ellas como coordenadas se obtiene la curva ROC.
En la Tabla 4 se ven las cifras de probabilidad pronosticada que aparecen después de estudiar los 300 pacientes y número de veces que se repiten.
En las Tablas 5 y 6 aparecen los tests de Hosmer- Lemeshow practicados en el trabajo actual y en el anterior. Se observa que en ambos hay aproximación entre los valores reales y los teóricos o sea entre observados y esperados.
En la figura 1 se puede ver la curva ROC obtenida al contrastar las cifras de probabilidad pronosticada de la Tabla 3 con la variable dependiente dificultad de intubación.
En la figura 2 se distinguen las dos cajas que reflejan la distribución de las probabilidades pronosticadas en los casos con dificultad de intubación y en los casos sin dificultad de intubación. Se visualizan las medianas y su diferente altura en cada caja y los valores periféricos (outliers) en la primera.
Para aplicar el modelo a cualquier paciente con los coeficientes obtenidos en la tabla 2: f(x) = 1,371 + 2,481 Laringoscopia Indirecta (3-4) + 2,181 Distancia Tiromentoniana < 6,5cm + (-1,484* cm Apertura Boca), lo haríamos así: tenemos un paciente que presenta una LI de 2 (comisura posterior y epiglotis visible), una DTM < 6,5 cm y una Apertura de Boca boca de 3 cm; f(x) = 1,371 + 2,181 DTM < 6,5 cm + (-1,484* 3 apertura boca).
Realizamos la operación y el resultado es =-0,900. Abrimos Excel vamos a la barra de fórmulas e insertamos la función fx=EXP(-0,900)/(1+EXP(-0,900)). Resolvemos y nos da como resultado: 0,2890505. Casi coincide con el resultado observado en la Tabla 4 en 5 pacientes: 0,28890, con esas mismas variables en la ecuación. Esa cifra es superior a 0,0498811 luego podemos prever una dificultad de intubación.
Tabla 1.
Variables introducidas en la ecuación.
| Puntuación | gl | Sig. | |||
| Variables | sexo(1) | ,512 | 1 | ,474 | |
| edad | ,023 | 1 | ,879 | ||
| índicemas | ,146 | 1 | ,702 | ||
| distatiroment | 12,113 | 1 | ,001 | ||
| aperturboca | 10,623 | 1 | ,001 | ||
| tamañcuel | ,118 | 1 | ,731 | ||
| roncador2(1) | ,648 | 1 | ,421 | ||
| retrognatia2(1) | 14,923 | 1 | ,000 | ||
| DTM(1) | 28,340 | 1 | ,000 | ||
| Aperturaboca(1) | 7,535 | 1 | ,006 | ||
| Grosorcuello43(1) | ,012 | 1 | ,911 | ||
| IMCmayor30(1) | 1,090 | 1 | ,296 | ||
| Movilidadcervical(1) | 3,645 | 1 | ,056 | ||
| Previstomall(1) | 7,035 | 1 | ,008 | ||
| epaba(1) | 4,293 | 1 | ,038 | ||
| ALH2(1) | 1,982 | 1 | ,159 | ||
| Pronosticodificint(1) | 25,301 | 1 | ,000 | ||
| Estadísticos globales | 65,171 | 17 | ,000 | ||
DTM:distancia tiro-mentoniana, epaba: epiglotis abaquillada, ALH: amígdala lingual hipertrófica.
Tabla 2
Predictores clínicos independientes de la DIO.
| B | Sig. | Exp(B) | |||
| aperturboca | -1,484 | 0,017 | ,227 | ||
| DTM(1) | 2,181 | 0,001 | 8,853 | ||
| Pronosticodificint(1) | 2,481 | 0,000 | 11,950 | ||
| Constante | 1,371 | 0,561 | 3,938 | ||
Tabla 3.
Coordenadas de la curva ROC
| Probabilidad pronosticada | Sensibilidad | 1 – Especificidad |
| ,0000000 | ,000 | ,000 |
| ,0008280 | ,014 | ,000 |
| ,0014357 | ,049 | ,000 |
| ,0020513 | ,056 | ,000 |
| ,0028796 | ,185 | ,000 |
| ,0035370 | ,189 | ,000 |
| ,0042984 | ,196 | ,000 |
| ,0053210 | ,437 | ,000 |
| ,0080046 | ,444 | ,000 |
| ,0117691 | ,643 | ,143 |
| ,0140474 | ,647 | ,143 |
| ,0154157 | ,657 | ,143 |
| ,0172332 | ,661 | ,143 |
| ,0194707 | ,671 | ,143 |
| ,0209180 | ,678 | ,143 |
| ,0243971 | ,790 | ,143 |
| ,0279862 | ,804 | ,143 |
| ,0324947 | ,808 | ,143 |
| ,0392206 | ,811 | ,143 |
| ,0429441 | ,818 | ,143 |
| ,0498811 | ,843 | ,143 |
| ,0701119 | ,857 | ,214 |
| ,0974566 | ,892 | ,214 |
| ,1363323 | ,927 | ,429 |
| ,1808944 | ,948 | ,500 |
| ,2031169 | ,951 | ,500 |
| ,2067903 | ,951 | ,571 |
| ,2479753 | ,972 | ,571 |
| ,3163844 | ,983 | ,714 |
| ,3490162 | ,986 | ,714 |
| ,4390665 | ,993 | ,714 |
| ,6110032 | 1,000 | ,786 |
| 1,0000000 | 1,000 | 1,000 |
Tabla 4
Probabilidad pronosticada.
| Probabilidad pronosticada | Frecuencia | Porcentaje | |
| ,00053 | 4 | 1,3 | |
| ,00112 | 10 | 3,3 | |
| ,00175 | 2 | ,7 | |
| ,00235 | 37 | 12,3 | |
| ,00341 | 1 | ,3 | |
| ,00367 | 2 | ,7 | |
| ,00493 | 69 | 23,0 | |
| ,00571 | 2 | ,7 | |
| ,01030 | 59 | 19,7 | |
| ,01324 | 1 | ,3 | |
| ,01485 | 3 | 1,0 | |
| ,01598 | 1 | ,3 | |
| ,01849 | 3 | 1,0 | |
| ,02045 | 2 | ,7 | |
| ,02138 | 32 | 10,7 | |
| ,02741 | 4 | 1,3 | |
| ,02856 | 1 | ,3 | |
| ,03643 | 1 | ,3 | |
| ,04201 | 2 | ,7 | |
| ,04388 | 7 | 2,3 | |
| ,05589 | 5 | 1,7 | |
| ,08434 | 10 | 3,3 | |
| ,11058 | 13 | 4,3 | |
| ,16209 | 7 | 2,3 | |
| ,19970 | 1 | ,3 | |
| ,20653 | 1 | ,3 | |
| ,20705 | 6 | 2,0 | |
| ,28890 | 5 | 1,7 | |
| ,34386 | 1 | ,3 | |
| ,35417 | 2 | ,7 | |
| ,52397 | 3 | 1,0 | |
| ,69804 | 3 | 1,0 | |
| Total | 300 | 100,0 | |
Tabla 5
Tabla de contingencias para la prueba de Hosmer y Lemeshow. Se observa intervalo por intervalo lo esperado y lo observado en el ensayo actual para cada uno de los dos resultados posibles de la variable dependiente dicotómica (dificultad de intubación o no).
| Dificultadintubacion = no dificultad | Dificultadintubacion = dificultad | Total | |||||||||
| Observado | Esperado | Observado | Esperado | ||||||||
| 1 | 16 | 15,983 | 0 | ,017 | 16 | ||||||
| 2 | 37 | 36,913 | 0 | ,087 | 37 | ||||||
| 3 | 3 | 2,989 | 0 | ,011 | 3 | ||||||
| 4 | 69 | 68,660 | 0 | ,340 | 69 | ||||||
| 5 | 2 | 1,989 | 0 | ,011 | 2 | ||||||
| 6 | 57 | 58,393 | 2 | ,607 | 59 | ||||||
| 7 | 42 | 41,146 | 0 | ,854 | 42 | ||||||
| 8 | 29 | 28,311 | 1 | 1,689 | 30 | ||||||
| 9 | 31 | 31,617 | 11 | 10,383 | 42 | ||||||
Prueba de Hosmer y Lemeshow en el ensayo actual.
| Paso | Chi cuadrado | gl | Sig. | |||
| 4,912 | 7 | ,671 | ||||
Tabla 6
Tabla de contingencias para la prueba de Hosmer y Lemeshow en el ensayo anterior. Se observa intervalo por intervalo lo esperado y lo observado para cada uno de los dos resultados posibles de la variable dependiente dicotómica (dificultad de intubación o no).
| Paso 3 | Dificultadintubacion = no dificultad | Dificultadintubacion = dificultad | Total | ||||||||
| Observado | Esperado | Observado | Esperado | ||||||||
| 1 | 223 | 223,054 | 2 | 1,946 | 225 | ||||||
| 2 | 29 | 27,852 | 1 | 2,148 | 30 | ||||||
| 3 | 25 | 26,041 | 4 | 2,959 | 29 | ||||||
| 4 | 9 | 9,054 | 7 | 6,946 | 16 | ||||||
Prueba de Hosmer y Lemeshow en el ensayo anterior.
| Paso | Chi cuadrado | gl | Sig. | |||
| 3 | 1,071 | 2 | ,586 | |||
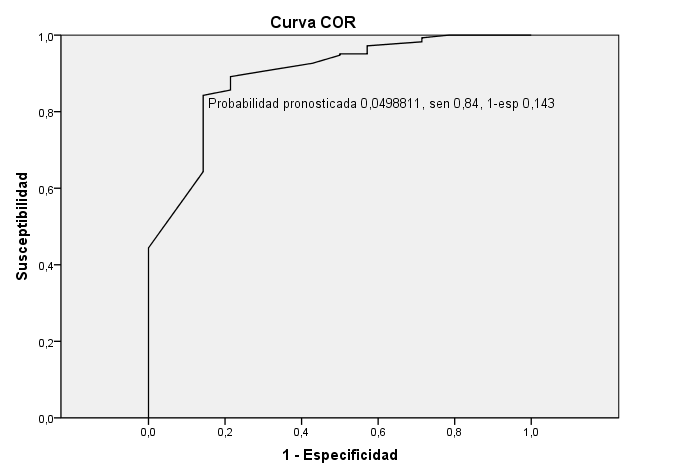
Figura 1. Curva de función operativa (ROC) de la probabilidad pronosticada “y”, obtenida en cada paciente de encontrar una dificultad de intubación. Se marca el punto de corte más cercano al ángulo superior izquierdo al que le corresponde una probabilidad pronosticada de 0,0498811, con una sensibilidad del 84 % y una cifra de 1-especificidad del 14 %. El área bajo la curva es del 89 %, sen = sensibilidad, esp = especificidad. Figure 1. Operative function curve (ROC) of the predicted probability «y», obtained in each patient to find an intubation difficulty. The cut-off point closest to the upper left corner is marked with a predicted probability of 0.0498811, with a sensitivity of 84% and a 1-specificity figure of 14%. The area under the curve is 89%, sen = sensitivity, esp = specificity.
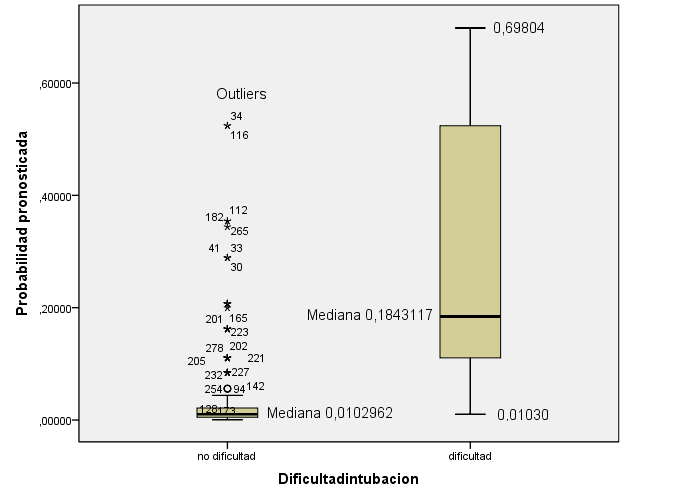
Figura 2. Se advierte en la primera caja que 10 pacientes sin dificultad de intubación presentan una probabilidad pronosticada por encima de la mediana de los pacientes con dificultad de intubación. En la segunda caja se expresan las cifras de probabilidad pronosticada máxima y mínima, esta última muestra la existencia de pacientes con dificultad de intubación con una probabilidad muy baja. Figure 2. It is noted in the first case that 10 patients without difficulty of intubation have a predicted probability above the median of patients with intubation difficulty. In the second box the maximum and minimum predicted probability figures are expressed, the latter shows the existence of patients with difficulty of intubation with a very low probability.
Discusión.
Vamos a observar e interpretar las diferencias con el estudio anterior2 debidas a la introducción de variables cuantitativas en el análisis de regresión logística (Tabla 1). En primer lugar observamos que aunque las variables en la ecuación son las mismas, cambian sus coeficientes y como consecuencia en la Tabla 2 podemos ver que la odd ratio (Exp(B)) de la LI es 11,95, un poco inferior a la encontrada anteriormente (13,02), también aquí esta cifra es la mayor de la tabla. La DTM sigue a la LI en cuanto a coeficiente. Pero existe un cambio en cuanto a la variable Apertura de la Boca, que ahora corresponde a la variable cuantitativa y su coeficiente es = -1,484 que hemos de multiplicar por los cm correspondientes, siendo una cifra negativa.
En la Tabla 3 se observa que para una misma cifra de 1-especificidad: 0,143 se corresponden no dos distintas cifras de sensibilidad como anteriormente, sino 12, se escoge como punto de corte aquella cifra de probabilidad pronosticada con sensibilidad más alta y más cercana al ángulo izquierdo del gráfico.
Comparando la Tabla 4 de este estudio con el anterior, en este se observa una mayor variedad en las cifras de probabilidad pronosticada, siguiendo con el ejemplo expuesto en Resultados vemos que 0,2890 se repite 5 veces y si vamos a los casos concretos observamos que en todos ellos las variables alteradas son la DTM y la Apertura de la Boca y que los 5 casos coinciden la DTM en cm y la Apertura de la Boca en cm o sea el SSPS ha tenido en cuenta las variables cuantitativas para realizar sus cálculos y no sólo las variables categóricas DTM < 6,5 y Apertura de Boca <3,5.
En las tablas 5 y 6 se observa que existe coincidencia entre los valores observados y los predichos, este test es más necesario cuando en el modelo se incluye una variable cuantitativa, como es el caso en el ensayo actual (tabla 5).
En la curva ROC (Figura 1) el mejor punto de corte correspondería a y = 0,0498811 (anteriormente2 y = 0,0626946) en la que el 84 % (sensibilidad: porcentaje de verdaderos positivos) de los pacientes con dificultad de intubación son detectados, con una proporción de falsos positivos del 14 %, el área bajo la curva es del 89 %, igual que en el anterior estudio, esto quiere decir que tenemos un 89 % de posibilidades en ambos ensayos de que acertemos en la clasificación de que un paciente presente o no una dificultad de intubación. En el estudio previo la sensibilidad era del 80 %, la cifra de 1-especificidad coincide con el anterior estudio. Se observa que se mejora en la detección de verdaderos positivos y que el punto de corte es inferior. Aunque en nuestro caso nos interesa sobre todo identificar a los verdaderos positivos y convendría escoger un punto de corte con una mayor cifra de “y”, pero esto conlleva un aumento de encontrarnos con falsos positivos, se comprende que estos lo son porque aparentando ser un paciente con una intubación difícil por presentar una cifra alta de “y” son ficticios.
En la figura 2 se contempla en la caja de pacientes con que alguna dificultad de intubación nos presentan una cifra muy baja de y =0,01057, en concreto son el 77 y el 243 que coinciden con el trabajo anterior cuya y = 0.00865.
En la otra caja se observan los outliers pacientes con una probabilidad pronosticada alta de presentar unadificultad de intubación y no la presentan (falsos positivos), de ellos 10 presentan una “y” por encima de la mediana de los pacientes con dificultad de intubación, 2 de estos presentan una y= 0,52397 son el 34 y el 116 (en el artículo anterior la y = 0,53694), que coinciden con los del trabajo anterior, aunque antes eran 4 los que presentaban esta cifra tan alta de “y”. Como ya se comentó estos dos pacientes no fueron fáciles de intubar, pero al presentar menos de 3 maniobras de intubación no fueron incluidas en el grupo de dificultad de intubación.
La inclusión de las variables cuantitativas mejora nuestros resultados, esto se aprecia en las tablas que son más completas y en el gráfico de cajas y la curva ROC.
En términos prácticos la DTM y la apertura de la boca son las variables que más influyen en la intubación difícil, en el ejemplo puesto en el apartado resultados, vemos que la cifra obtenida en ese paciente (0,28905050) coincidía con cinco pacientes del estudio (28890, tabla 4), esa cifra presenta una tasa de falsos positivos entre el 57 y el 71 por ciento (tabla 3). Vamos a repasar estos pacientes, vemos que dos de ellos presentaron dificultad de intubación (nº177 y 188) tres no (nº 30, 33 y 41) aunque el nº 30 precisó presión cricotiroidea (dos intentos de intubación) para poder visualizar la glotis y fue dificultosa la ventilación con mascarilla facial, o sea tres fueron falsos positivos, el 60 % de 5.
Si a la disminución de la DTM y de la apertura de la boca, se añade la dificultad de visión mediante LI (influenciada a su vez por la falta de movilidad cervical y la roncopatía3), se puede razonar que un paciente que manifieste todas estas alteraciones va a ser posiblemente subsidiario de una intubación difícil, sobra la práctica de la LI y el esfuerzo de artículos que inciden en lo ya conocido. Pero todo esto, que cualquier practicante de la anestesia sabe por artículos precedentes y por su propia experiencia, hay que intentar ampliarlo, aquí se añade la LI a las variables a investigar, se postula como aplicar nuestros resultados a cualquier paciente y se estudian las limitaciones del método y como mejorarlo. Nuestro deber como investigadores es aproximar la medicina a la ciencia, hasta donde los conocimientos actuales lo permitan.
Bibliografía.
1.- Molina Arias M. Una relación simple. Modelos de regresión simple. Rev electron AnestesiaR 2016. Agosto.
2.- www.mianestesia.es/prediccion-dificultad-intubacion/potencia de la laringoscopia indirecta incluida en un método de predicción de dificultad de intubación aplicable a cualquier paciente.
3.- Sánchez Morillo J, Estruch Pérez MJ, Hernández Cádiz MJ, Tamarit Conejeros JM, Gómez Diago L, Richard Aznar M. La laringoscopia indirecta mediante laringoscopio rígido de 70º como valor predictivo de la dificultad de visión de la laringe. Acta Otorrinolaringol Esp. 2012; 63(4):272-9.
